Constructing square root 2 for lower sec

Squares 


In the secondary 1/2 syllabus for math, we talk about numbers. For instance, rational numbers and irrational numbers. Now how can we show the students a line segment of length square root 2? Moreover, these students need not have prior knowledge of pythagoras' theorem. So showing them an isoceleles triangle with 2 sides 1 and hypothenus sqrt2 may not be the best way to go.

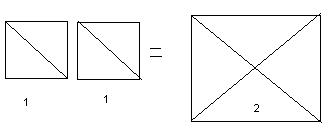
Let us consider 2 squares each of length 1. So each has area 1 (unit, can be cm, m or anything else to make things concrete, I'll just discuss in abstract) Question: From these 2 squares, can you construct a square of area 2?

The above diagram represents the solution. Cut the 2 small squares into half along the diagonal and piece them together to form the square on the right. That square will be of area 2. So the length of the square is sqrt2. And hence we have demonstrated the construction of a line segment of sqrt2 without using any fancy maths.